This tutorial explains how to calculate geocentric RIGHT ASCENSION (R.A.) & DECLINATION for the Moon.
The JS simulation will also use these calculated coordinates to plot the Moon on the Celestial Sphere as well as show the percentage of the illuminated disc.
This tutorial is unrelated to the first three tutorials in the series, and can be followed independently.
However, the orbit of the Moon is perturbed by the Sun and Earth which requires various corrections.
If you haven't followed the third tutorial yet for calculating the Epheremis for the Sun and the Planets, we recommend you do that first: TUTORIAL - EPHEMERIS PLANETS
Credits for all calculations go to Jean Meeus, as this example was taken directly from his book Astronomical Algorithms.
If you have the book at hand, you can follow along in Chapter 47 (Position of the Moon).
I. CALCULATE CENTURIES SINCE EPOCH J2000.0
All calculations in this tutorial are based on the J2000.0 epoch (JD = 2451545). The value of time "T" is measured in Julian centuries since the Epoch J2000.0.For a refresher on how to convert a Gregorian Date to a Julian Date, see our first tutorial: TUTORIAL - PLANETS
Once you have converted the desired Julian Ephemeris Day, use this formula to calculate time "T":
//Time "T" is centuries since J2000.0
T = (Julian Ephemeris Day - 2451545) / 36525
II. CALCULATE MOON & SUN ANGLES
Now that we know the value T, we can calculate the following angles (taken from Meeus):- MOON MEAN LONGITUDE
L' = 218.3164477 + (481267.88123421 * T) - (0.0015786 * Math.pow(T,2)) + (Math.pow(T,3) / 538841) - (Math.pow(T,4) / 65194000);
D = 297.8501921 + (445267.1114034 * T) - (0.0018819 * Math.pow(T,2)) + (Math.pow(T,3) / 545868) - (Math.pow(T,4) / 113065000);
M = 357.5291092 + (35999.0502909 * T) - (0.0001536 * Math.pow(T,2)) + (Math.pow(T,3) / 24490000);
M' = 134.9633964 + (477198.8675055 * T) + (0.0087414 * Math.pow(T,2)) + (Math.pow(T,3) / 69699) - (Math.pow(T,4) / 14712000);
F = 93.2720950 + (483202.0175233 * T) - (0.0036539 * Math.pow(T,2)) - (Math.pow(T,3) / 3526000) + (Math.pow(T,4) / 863310000);
Ω = 125.04452 - (1934.136261 * T) + (0.0020708 * Math.pow(T,2)) + (Math.pow(T,3) / 450000);III. CALCULATE MOON LATITUDE & LONGITUDE
To calculate the Moon's Latitude and Longitude, the angles calculated in SECTION II are used in a so-called "linear combination" using a table of periodic terms. A linear combination represents the sum of the fundamental arguments D, M, M' & F with a coefficent placed in front of it as a multiplier.Next to that, some of these terms also require the Earth's eccentricity of its orbit around the Sun:
E = 1 - (0.002516 * T) - (0.0000074 * Math.pow(T,2));After calculating the periodic terms for the Moon, several "additive terms" are applied (A1, A2 & A3). The last step is to calculate the coordinates of the Moon using the following formula's (taken from Meeus):
//Geocentric Longitude Moon
λ = L' + ∑l / 1000000
//Geocentric Latitude Moon
β = L' + ∑b / 1000000IV. CALCULATE LONGITUDE & OBLIQUITY NUTATION
To get a more accurate value for the Moon's position, we need to take into account the phenomenon of nutation. For additional information see the NUTATION section in the GLOSSARY. This nutation adjustment will be applied to the Moon's Longitude (λ) and the Obliquity of the Ecliptic (ε).The values for △ψ (nutation in longitude) and △ε (nutation in obliquity) are again calculated using linear combination with a table of periodic terms. Please refer again to the SOURCE CODE for details.
V. CALCULATE MEAN & TRUE OBLIQUITY
We first need to calculate the MEAN OBLIQUITY. The formula is:
ε0 = 23.43929 - (0.01300417 * T) - (0.0000001638889 * Math.pow(T,2)) - (0.0000005036111 * Math.pow(T,3));
ε = ε0 + △εVI. CONVERT ECLIPTIC TO EQUATORIAL COORDS.
Now use the following formula's to convert the ecliptical coordinates calculated in SECTION III and corrections from SECTION IV and SECTION V into equatorial coordinates to acquire the RIGHT ASCENSION & DECLINATION:
tan α = ((sin λ * cos ε) - (tan β * sin ε)) / (cos λ) //RIGHT ASCENSION
sin δ = (sin β * cos ε) + (cos β * sin ε * sin λ) //DECLINATION
VII. SIMULATOR ACCURACY
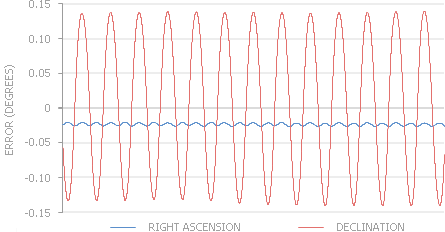 To get a better idea of the accuracy of this method to calculate the position of the moon, the results are plotted against NASA's HORIZONS Web-Interface for the year 2025.
To get a better idea of the accuracy of this method to calculate the position of the moon, the results are plotted against NASA's HORIZONS Web-Interface for the year 2025.
The graph displays the error in degrees for both the RIGHT ASCENSION and DECLINATION. This error translates roughly to a maximum of 3 minutes for RIGHT ASCENSION and 9 minutes for DECLINATION.
VIII. CALCULATE ILLUMINATED FRACTION OF DISK
Using the Moon and Sun angles calculated in SECTION II, we can also calculate the Moon's illuminated fraction. The JavaScript implementation below returns the illuminated fraction as a number between 0.0 and 1.0:
function calculateMoonIlluminatedFraction(){
i = 180 - moonMeanElongation - (6.289 * Math.sin(moonMeanAnomaly)) + (2.100 * Math.sin(sunMeanAnomaly))
- (1.274 * Math.sin(2*moonMeanElongation - moonMeanAnomaly)) - (0.658 * Math.sin(2 * moonMeanElongation))
- (0.214 * Math.sin(2 * moonMeanAnomaly)) - (0.110 * Math.sin(moonMeanElongation));
k = (1 + Math.cos(i)) / 2;
return k;
}
Since the phase of the Moon is identical all around the world, you can use this function to figure out the next full Moon.
IX. COMPLETE JS LUNAR EPHEMERIS SIMULATOR
The apparent "sine wave" motion is caused by the axial tilt of the Earth (see "PATH OF SUN ACROSS SKY" section in GLOSSARY).
Get the full JavaScript source code HERE.
You can also verify the RIGHT ASCENSION and DECLINATION values using NASA's HORIZONS Web-Interface. Make sure to set the Observer Location to "Geocentric [500]" for comparison.
Want to learn more? Explore our JavaScript tutorial for calculating the position of the Moon for a specific location on Earth HERE.